AO modulators

The acoustooptic effect allows controlling any parameters of an optical wave: amplitude, phase, frequency and polarization. Therefore, different modifications of the acoustooptic modulators can be realized. Besides, it should be taken into account that acoustooptic interaction makes it possible to introduce information into an optical beam by means of both temporal and spatial modulation.

At the present time, the temporal modulators of light intensity are the most widespread. These modulators employ a progressive acoustic wave modulated in amplitude by an informative signal. The principle of operation of the modulators is based on the dependence of the diffracted light intensity 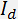on the acoustic power 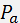. A scheme of the modulator operating in the Bragg regime of diffraction is shown in Fig. 1m. 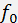Electrical oscillations of a frequency from a HF generator (1) are modulated in amplitude by an informative signal 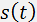and then enter a piezotransducer (2) of an acoustooptic cell (3). The regime of travelling acoustic waves is provided by an acoustic absorber (4). The carrier frequency 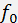is chosen equal to the central frequency of the transducer. Modern technology permits attaining the transducer bandwidth 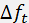as great as 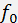; so that

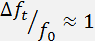
A basic characteristic of the modulator is the modulation bandwidth 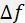. It is obvious that 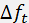cannot be greater than 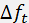. However, there exist additional restrictions of the modulation band defined by peculiarities of acoustooptic interaction. 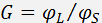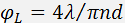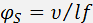For the modulators, the parameter is of considerable importance, where and are the optical and acoustic beam divergences, $\lambda$ is the optical wavelength in vacuum, $n$ s the refractive index, $\nu$ is the acoustic velocity, $f$ is the acoustic frequency, $d$ and $l$ are the optical and acoustic beam widths in the acoustooptic interaction plane. If the condition 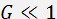is satisfied, the modulation bandwidth is determined by the relationship 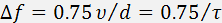. This expression shows that in the limit $G\to 0$ the modulation band is defined exclusively by the time $\tau$ required for ultrasound to cross the optical beam. With increasing the parameter $G$ the modulation band becomes narrower because of volume effects in acoustooptic interaction. In this case the ratio 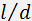plays the decisive role.

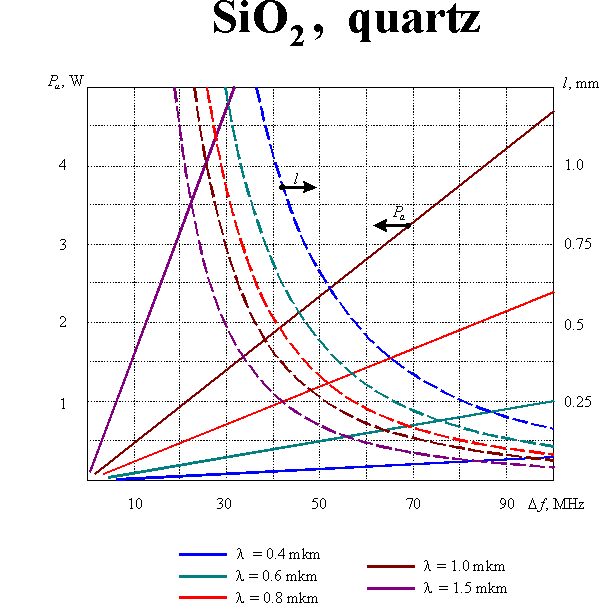
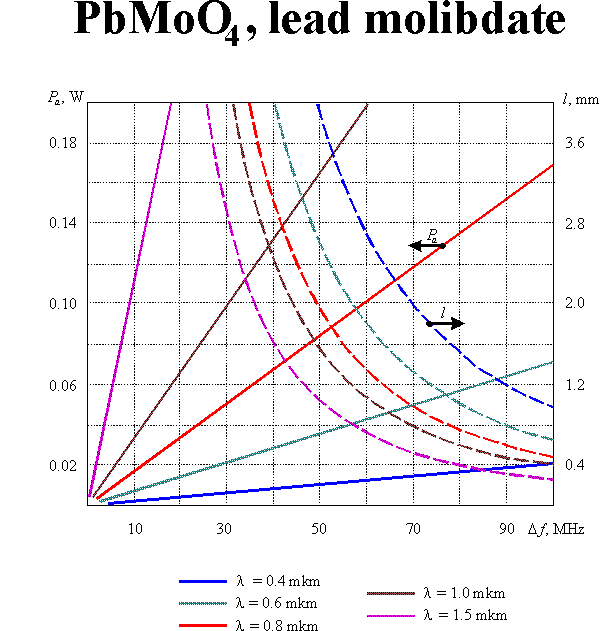
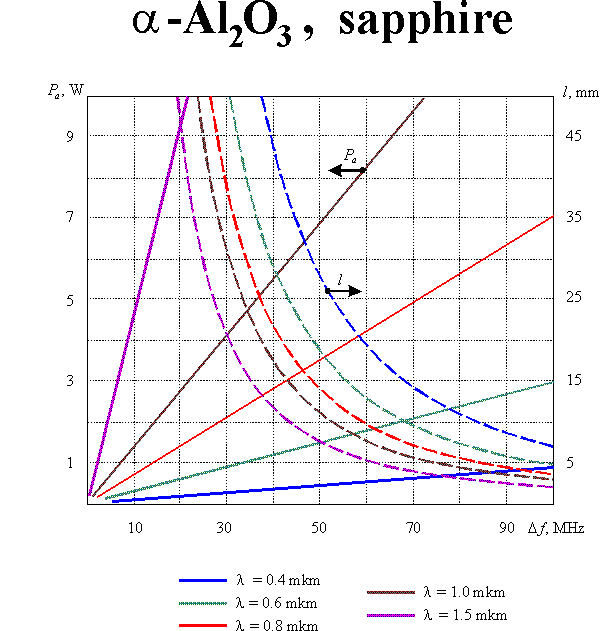
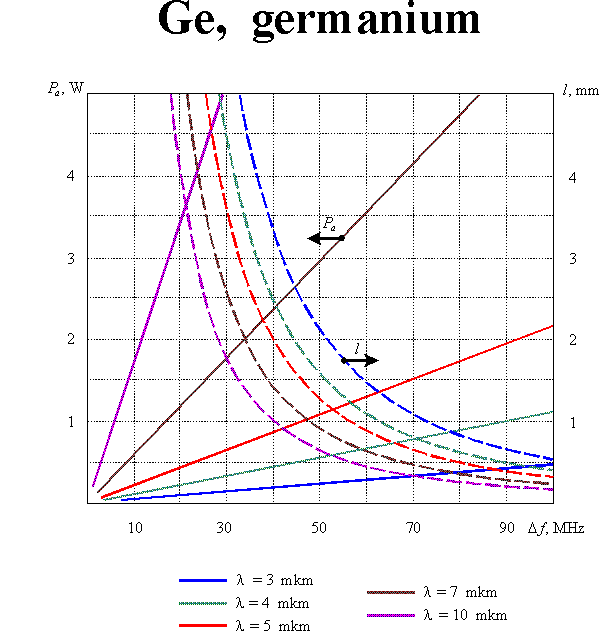
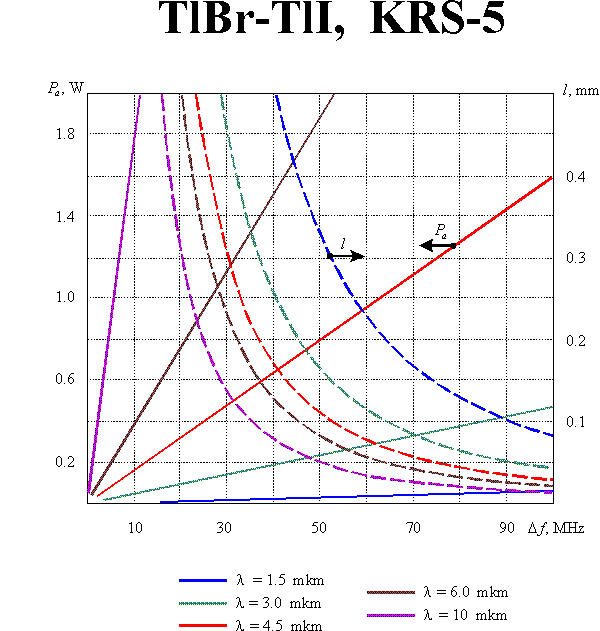
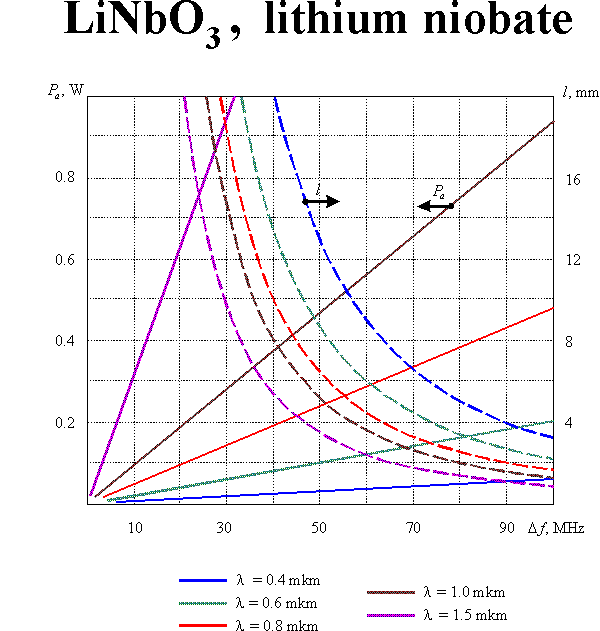
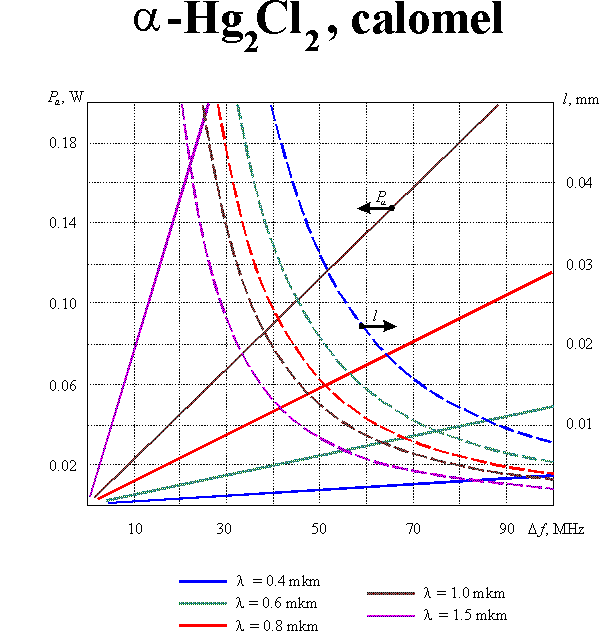
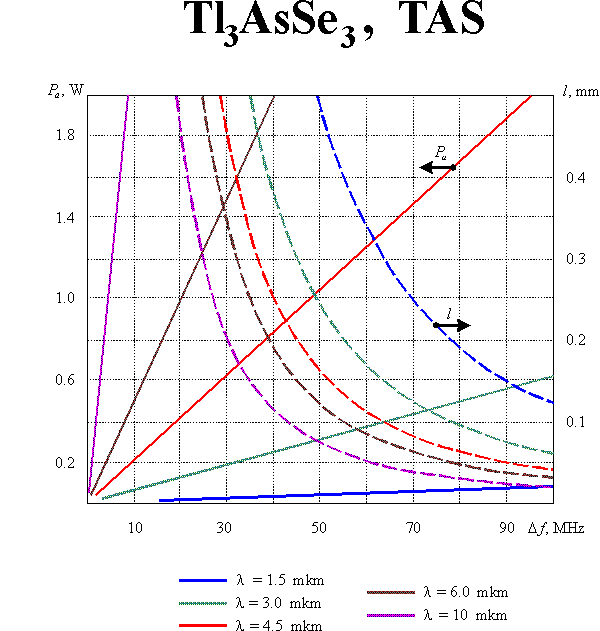
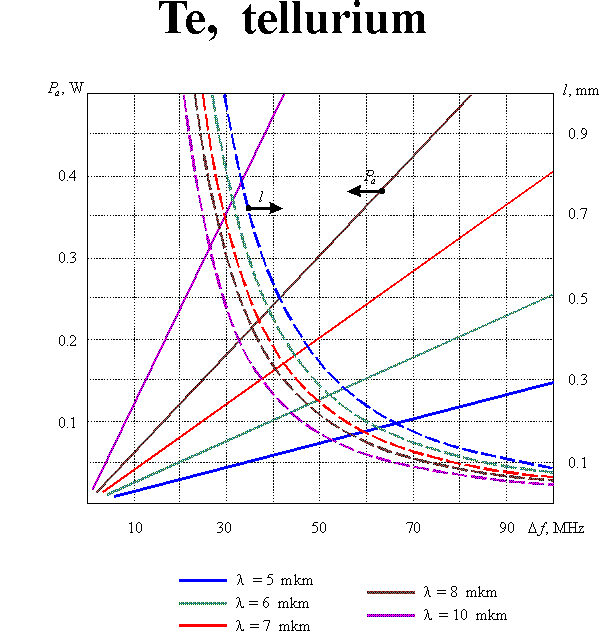
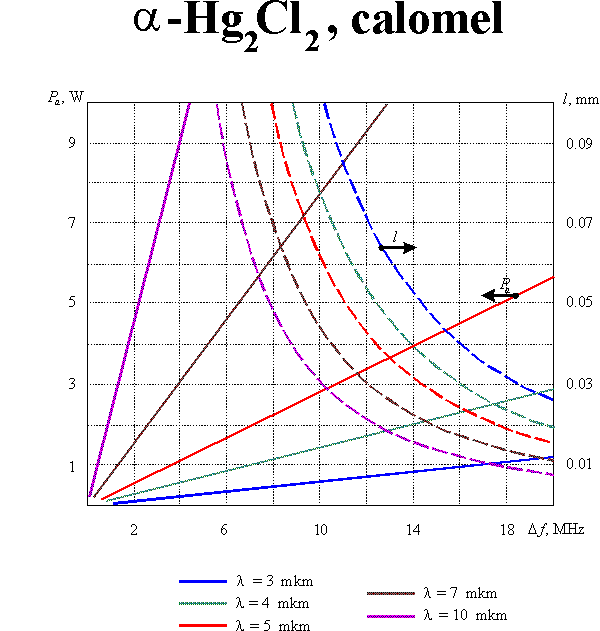
The optimization of modulator parameters is conventionally produced with taking into consideration both the modulation band and the consumed power. Such optimization leads to the following value of the parameter $G$: $G\approx 1$ which defines the condition of optical and acoustic beam divergences matching. In this case

If the diffraction efficiency $\zeta$ does not exceed 30%, the consumed acoustic power 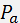can be calculated from the equation

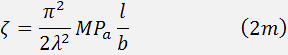
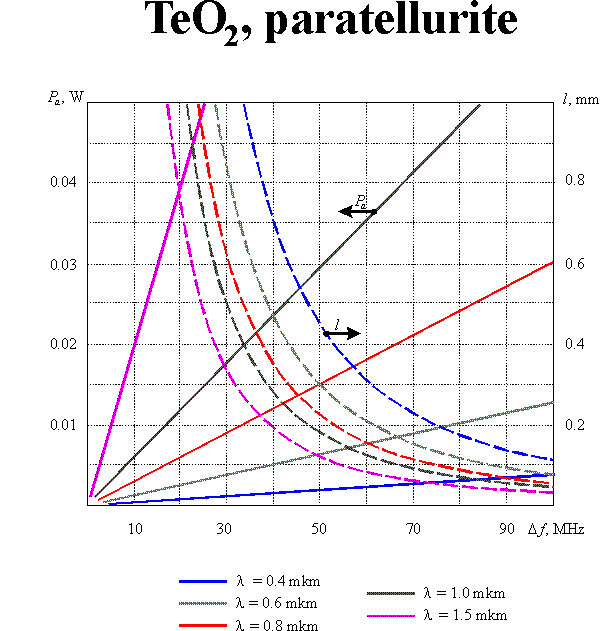
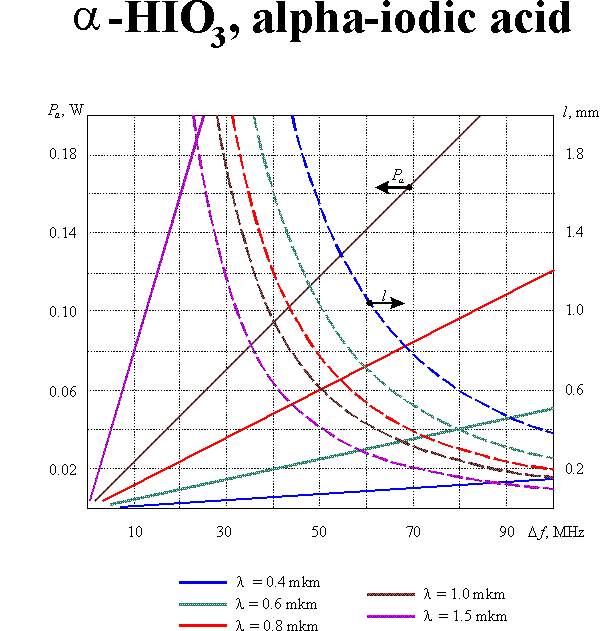
where $M$ is the acoustooptic figure of merit, $l\times b$ is the cross-section of the acoustic beam. Eqs (1m) and (2m) enable defining optimal parameters of the modulating acoustooptic cell. Supposing the acoustic bandwidth $\Delta f$ to given, one can yield:

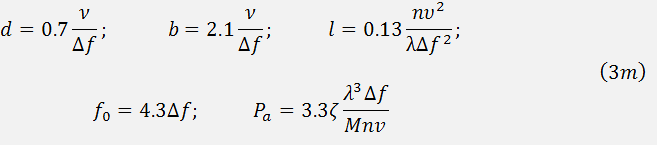
Here the reasonable assumptions 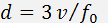and 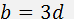are taken into account. Graphic results of the calculations for $\zeta$ equal to 30% and for different acoustooptic materials are presented in this section.