AO effect

Acousto-optic effect, also known in the scientific literature as acousto-optic interaction or diffraction of light by acoustic waves, was first predicted by Brillouin in 1921 and experimentally revealed by Lucas, Biquard and Debye, Sears in 1932.

The basis of the acousto-optic interaction is a more general effect of photoelasticity consisting in the change of the medium permittivity 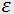under the action of a mechanical strain 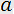. Phenomenologically, this effect is described as variations of the optical indicatrix coefficients 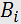caused by the strain :

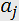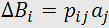
where 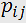is the photoelastic tensor components .

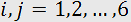In case of the acousto-optic effect, the strains 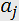are produced by an acoustic wave excited in a transparent medium. Thus, one can say that the acoustic wave is accompanied by a wave of refractive index variations. For a plane acoustic wave propagating along the axis Z, one can write that

,

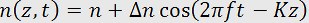where n is the undisturbed index of refraction, f and K are the frequency and propagation constant of the acoustic wave, 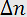is the amplitude variation of the refractive index induced by the acoustic wave:

,

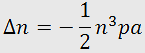For the light, the medium with the refraction index 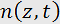represents a phase grating moving with the sound velocity V. Passing the medium, the light diffracts on inhomogeneities of the refraction index, forming in the far field a salient diffraction pattern.

On examination of light diffraction by a monochromatic acoustic wave, two limiting regimes are distinguished first of all – the regimes of Raman-Nath and Bragg. The Raman-Nath regime is observed at relatively low acoustic frequencies f and a small acoustooptic interaction length l (typically, 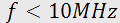and 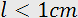). This type of diffraction takes place at an arbitrary incidence angle of light 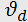(Fig. 1,a). The diffraction pattern can contain many diffraction orders with symmetrical distribution of light intensity. By contrast, the Bragg regime is observed at high acoustic frequencies exceeding usually 100MHz. The diffraction pattern, even at a large acoustic power 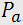, consists, as a rule, of two diffraction maxima of the

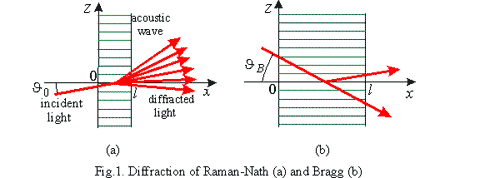
zeroth and first orders. However, even these maxima appear only at definite incidence angles near the so-called Bragg angle 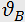(Fig. 1,b). In this case, the side maximum (Bragg maximum) is formed as a selective reflection of light from wave fronts of ultrasound. The Bragg angle is determined by the expression

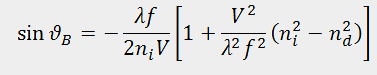
where 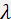is the optical wavelength in vacuum, 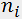and 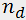are the refraction indices for the incident and diffracted light, respectively.

There is no well-defined boundary between these two diffraction regimes. With increasing the acoustic frequency the angular selectivity of acousto-optic interaction increases and the number of observed maxima is gradually reduced. Traditionally, the Raman-Nath and Bragg regimes are stated by the conditions 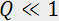and 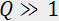accordingly, where

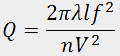
is the Klein-Cook parameter. Since only one diffraction maximum is used in acousto-optic devices (the first order, as a rule), the Bragg regime is more preferable because of smaller light losses. However, the acousto-optic selectivity peculiar to the Bragg diffraction restricts the frequency range of acousto-optic interaction and, as a consequence, speed of operation of acousto-optic devices.

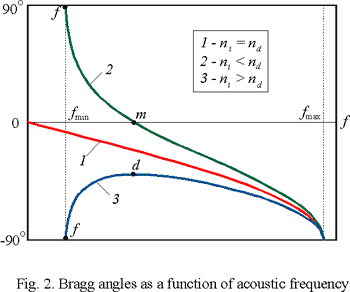
If the acoustooptic medium is optically isotropic, then refraction coefficients for incident and diffracted light beams are the same and equation for Bragg angle can be simplified to:

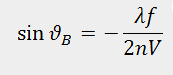
Curve 1 in Fig. 2 shows the dependence 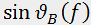for this case. In an anisotropic medium, two types of acousto-optic interaction are possible. If the optical mode does not change during the acousto-optic interaction, then 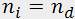(o => o type of scattering) or (e => e scattering) and the Bragg angle is determined by equation above. This type of acousto-optic interaction is known as isotropic diffraction. In the other case known as anisotropic diffraction, the optical mode is transformed during the diffraction process (o => e or e => o scattering). Therefore, 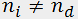and the dependence 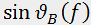becomes much more complicated. Curves 2 and 3 in Fig. 2 demonstrate these dependencies for a relatively simple variant when the acousto-optic interaction plane is perpendicular to the optical axis of an uniaxial crystal.

From the viewpoint of practical usage, all advantages of anisotropic diffraction result from these complicated dependences of the Bragg angle on the acoustic frequency. It has been shown that the best characteristics of acousto-optic deflectors are achieved in the region where 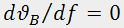(point d in Fig.2). Analogously, optimal areas for modulators and filters are situated close to points m and f, respectively, where 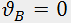and .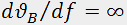

An analytical solution of the problem of acousto-optic interaction can be obtained only for the limiting cases of Raman-Nath and Bragg diffraction. In the latter case, assuming additionally that the optical beam falls on the acousto-optic cell at the Bragg angle, the following expression for the diffraction efficiency can be derived:

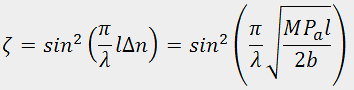
where l and b define the cross-section of the acoustic beam. The parameter M defined by the expression

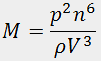
where 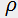is the medium density, is known as an acousto-optic figure of merit; it is the main parameter of the acousto-optic medium. The greater the figure of merit, the less the required acoustic power 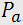to achieve the diffraction efficiency needed